GEOMETRIC CONSTRUCTIONS
E-mail: jay(at)salsburg(dot)com
Helpful Graphical solutions to common and not so common drafting problems.
A. The Straight Line and Its Division
1. To Divide a Line Segment into a Specified Number of Equal Parts
2. To Divide a Line Segment into a Given Ratio
3. To Construct a Line Segment Which is the Mean Proportional (Geometric
Mean) to Two Given Line Segments
4. To Divide a Straight Line in Extreme and Mean Proportion
B. The Construction of Triangles and Regular Polygons
1. To Construct a Triangle with Known Lengths of the Sides
2. To Construct a Right Triangle when the Lengths of the Hypotenuse and
One Side Are Known
3. To Inscribe an Equilateral Triangle within a Circle Having a Given Diameter,
AB
4. To Construct a Regular Pentagon when the Length AB of the Sides is Known
5. To Construct a Regular Pentagon when the Length EC of a Diagonal is known
6.. To Inscribe a Hexagon within a Given Circle
7. To Construct a Regular Polygon Having n Sides
C. Circles and Their Tangents
1. To Draw a Circle Through Three Given Points
2. To Inscribe a Circle in a Given Square, Using the Method of Intersecting
Rays
3. To Draw Lines Tangent to a Circle, and Passing Through a Given Point,
A
4. To Draw a Line Tangent to the Arc of a Circle, and Passing Through a
Given Point, P
5. To Draw Tangents to Two Given Circles
6. To Draw an Arc of Given Radius, r, Tangent to Two Given Lines m and n
7. To Draw Arcs of Radius r, Tangent to a Given Line, m, and a Given Circle,
O
8. To Draw Arcs of Radius r, Tangent to Two Given Circles
9. To Rectify a Circular Arc
10. To Divide a Circle into Seven Equal Parts by Concentric Circles
D. Conic Sections
The Ellipse.
1. To construct an ellipse when the foci F1 and F2 and the constant distant
AB are given
2. To draw an ellipse by the pin-and-string method when the major axis,
AB, and the minor axis, CD, are given
3. To draw an ellipse when two conjugate axes are given
4. To determine the major and minor axes, and the foci of a given ellipse
5. To draw an ellipse by the concentric circle method, given the lengths
of the major and minor axes
6. To draw an ellipse by the trammel method when the major and minor axes
are given
7. To draw an ellipse by the use of circular arcs when the axes are given
8. To inscribe an ellipse in a given rectangle
The Parabola.
1. To locate points on a parabola when the focus, F, and the directrix,
d, are given
2. To determine the axis, focus, and directrix of a given parabola
3. To construct a parabola, given the axis, vertex V, and a point P through
which the parabola passes
The Hyperbola.
1. To construct a hyperbola when the foci, F1 and F2, and the constant distance,
AB, are given
2. To construct a rectangular hyperbola (asymptotes are at right angles),
given the asymptotes m and n, and one point P on the curve
3. To construct a hyperbola, given the transverse axis AB, and a point P
on the curve
Pascal and His Theorem.
1. To locate a sixth point on a conic when five points are known
2. To locate points on a conic that passes through a given point and is
tangent to given lines at two points
3. To construct a tangent to a given conic at a point of the conic
Brianchon's Theorem
1. To determine a sixth tangent to a conic when five tangents (sides of
the circumscribed hexagon) are given
2. To determine the point of contact of a tangent to a conic
3. To determine additional tangents to a conic when four tangents and the
point of contact on one of them are known
4. To determine additional tangents to a conic when three tangents and the
points of contact on two of them are known
Additional Useful Geometric Constructions.
1. To draw a line through a given point, P, and the inaccessible copoint
of given lines m and n
2. To draw a line perpendicular to a given line AB and through the inaccessible
copoint of given lines m and n that pass through points A and B, respectively
3. To divide a given quadrilateral ABCD into two equal areas by a line which
passes through one of the corners, A
A. The Straight Line and Its Division
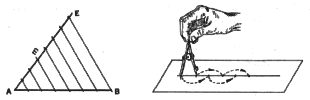
1. To Divide a Line Segment into a Specified Number of Equal Parts. Suppose
line segment ABis given and that it is required to divide AB into seven
equal parts.
Solution. Through point A draw line m and then lay off seven equal distances,
starting at point A. Join points E and B and then draw parallels to EB through
the points on m. The points of intersection of these parallels with line
segment AB divide it into the required seven equal parts. Why is this true?
Suggestion. In laying off distances on a line segment, use needle-point
dividers, alternating the rotation of the dividers as shown.
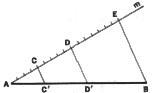
2. To Divide a Line Segment into a Given Ratio. Let AB represent the given
line segment, and let the given ratio be 4:5:7. Draw line m through point
A and at any convenient angle with AB. On m lay off distances AC = 4 units,
CD = 5 units, DE = 7 units. Draw BE and then draw lines through C and D
parallel to BE, cutting AB in points C' and D', which determine the required
segments of AB.
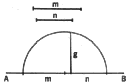
3. To Construct a Line Segment Which is the Mean Proportional (Geometric
Mean) to Two Given Line Segments. Suppose the given segments are m and n.
On line AB lay off consecutive segments equal to m and n. Construct a semicircle
on the total length (m + n) as a diameter. At the common point of the segments
construct a perpendicular to the diameter. Line g is the required mean proportional.
The student should prove this by showing that g squared = m X n.
4. To Divide a Straight Line in Extreme and Mean Proportion . The given
line is AB. At point B lay off line BC at 90° to AB and equal to AB/2.
With C as center and radius CB, draw an arc cutting line AC at point D.
With A as center and radius AD, draw an arc cutting line AB at point E,
which divides line AB in extreme and mean proportion (i.e., the square on
segment AEis equal to the rectangle having sides AB and EB).

B. The Construction of Triangles and Regular Polygons
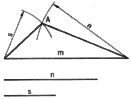
1. To Construct a Triangle with Known Lengths of the Sides. Suppose m, n,
and s are the given lengths. With the end points of m as centers and radii
equal to n and s, respectively, draw intersecting arcs, locating point A.
Join A with the end points of m to complete the construction of the triangle.
Is it possible to construct a triangle with 7, 3 1/2 and 3 inches as the
lengths?
2. To Construct a Right Triangle when the Lengths of the Hypotenuse and
One Side Are Known. Let line m and n represent the given lengths. Construct
a semicircle with diameter AB equal to length m. With A as center (could
use B) and radius equal to length n, draw an arc cutting the semicircle
at point C. Triangle ABC is the required right triangle. Why is this true?
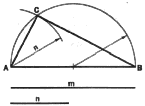
3. To Inscribe an Equilateral Triangle within a Circle Having a Given Diameter,
AB. With center O and radius equal to AM (M is midpoint of AB), draw the
circle. With C as center and the same length of radius, draw an arc cutting
the circle in points D and E. Join points D, E, and F. The required triangle
is DEF.
4. To Construct a Regular Pentagon when the Length AB of the Sides is Known.
First construct BC = AB, and perpendicular to AB. With M (midpoint of AB)
as center and MC as radius, draw an arc cutting AB extended at point D.
Now with A as center and AD as radius, draw an arc; and, with B as center
and radius BA, draw an intersecting arc to locate point E. Line BE is a
side of the regular pentagon. The construction for locating point F and
G is fairly obvious. ABEFG is the required pentagon. (The solution of this
problem is based upon the fact that the larger segment of a diagonal of
the pentagon, when divided in extreme and mean proportion, is the length
of a side of the pentagon. Note that point B divides AD in extreme and mean
proportion and that AB is the larger segment of AD.)
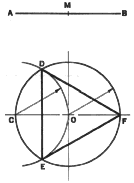
5. To Construct a Regular Pentagon when the Length EC of a Diagonal is known.
First divide EC in extreme and mean proportion (ET squared = EC X TC). With E and
C as centers and radius ET, draw arcs that intersect at point D. Draw the
perpendicular bisector of ED and locate point O on the vertical line passing
through D. Point O is the center of the circle (radius OE) which circumscribes
the pentagon.
With E and C as centers and a radius equal to CD (or ED), draw arcs cutting
the circle at points A and B. Draw the necessary lines to form pentagon
ABCDE.
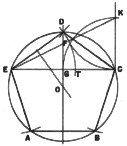
6. To Inscribe a Hexagon within a Given Circle.

With A and D as centers and a radius equal to the radius of the circle,
draw arcs which intersect the given circle in points B, F, C, and E. The
required hexagon is ABCDEF. An alternative construction is shown.
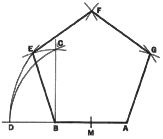
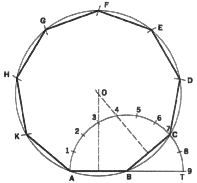
7. To Construct a Regular Polygon Having n Sides. The polygon in this example
is a nonagon (nine equal sides) and AB is the given length of each side.
With B as center and AB as radius, describe a semicircle, and by trial divide
it into nine equal parts. Starting from point T, locate the second division
mark, C. Locate point 0, the center of the circumscribing circle. (This
is easily done by finding the intersection of the perpendicular bisectors
of AB and BC.) Draw the circle with center O and radius OA and complete
the nonagon
 .
.
C. Circles and Their Tangents
1. To Draw a Circle Through Three Given Points. Let us assume A, B, and
C as the given points. Draw the perpendicular bisectors of lines AB and
BC. The intersections of the bisectors is point O, the center of the circle
which passes through the three given points.
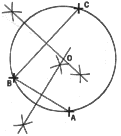
Now suppose that the center of the circle is inaccessible. Again the given
points are A, B, and C. Draw arcs with A and C as centers and radius equal
to A C. Now draw lines ABD and CBE. On arc AE lay off, from point E, relatively
short equal distances 1u, 2u, 3u, etc., above E, and similarly, equal distances
1L, 2L, 3L, etc., below E.
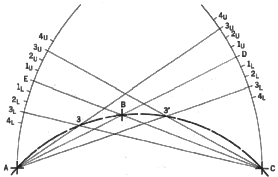
In like manner lay off distances 1u,, 2u, 3U, etc., above D and 1L, 2L,
3L, etc., below D. Now draw lines A-3u and C-3L. Their intersection is point
3. Similarly locate point 3' and, in like manner, additional points. The
required circle will pass through points A, 3, B, 3', and such additional
points as desired. (The proof is left to the reader.)
2. To Inscribe a Circle in a Given Square, Using the Method of Intersecting
Rays. If a plane parallel to the base of a right circular cone cuts the
cone, the intersection is a circle [Fig. (a)].
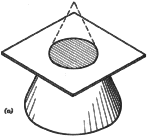
Points on the circle may be located by finding the intersection of rays
C-1, C-2, etc., drawn through point C [Fig. (b)],
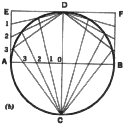
with the corresponding rays D-1, D-2, etc., drawn through point D. Rectangle
AEFB is half of the given square.
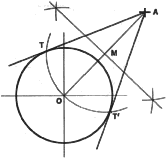
3. To Draw Lines Tangent to a Circle, and Passing Through a Given Point,
A. Locate point M, the midpoint of line OA. With M as center and radius
MO, draw an arc cutting the given circle at the points of tangency, T and
T'. The tangent lines are AT and AT'.
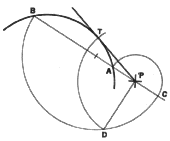
4. To Draw a Line Tangent to the Arc of a Circle, and Passing Through a
Given Point, P. First draw through point P secant line PAB. Extend this
line to point C such that PA = PC. Now find the mean proportional between
PA and PB. This is shown as PD. With P as center and radius PD, draw an
arc cutting the given arc at point T. Line PT is the required tangent. (The
construction shown is based on the fact that PT squared = PA X PB.)
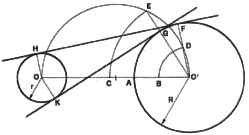
5. To Draw Tangents to Two Given Circles. On line O-O', which joins the
centers of the circles, lay off from O', distance O'B = (R-r), and O'C =
(R + r). With O' as center and radii O'B and O'C, draw arcs which intersect
the semicircle on O-O' at points D and E, respectively. Draw O'D to intersect
circle O' at F, and similarly draw O'E to intersect circle O' at G. Through
center O draw OH parallel to O'F and OK parallel to O'G. Lines FH and GK
are tangent to both circles.
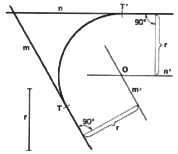
6. To Draw an Arc of Given Radius, r, Tangent to Two Given Lines m and n.
The center O of the required arc is at the intersection of lines m' and
n', which are parallel to lines m and n, respectively, at distance r. The
construction is clearly shown in the figure.
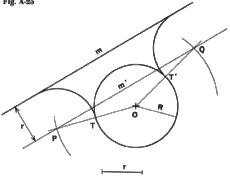
7. To Draw Arcs of Radius r, Tangent to a Given Line, m, and a Given Circle,
O. With O as center and radius (R + r), draw an arc cutting line m' (line
m' is parallel to m at distance r) at points P and Q, which are the centers
of the required arcs.
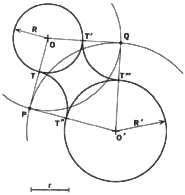
8. To Draw Arcs of Radius r, Tangent to Two Given Circles. With center O
and radius (R + r), draw an arc; and, with center O' and radius (R' + r),
draw an arc. The intersections of the two arcs are P and Q, which are the
centers of the required arcs.
9. To Rectify a Circular Arc. Arc Om in [Fig. (a)]
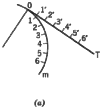
is first divided into a number of short equal segments, in this case 6.
These distances, such as 0-1, 1-2, etc., are laid off on tangent OT, as
0-1', 1'-2'', etc. Length 0-6' is (very nearly) the length of the arc from
0 to 6.
An alternative solution is shown in [Fig. (b)].
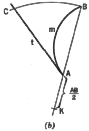
With K as center and KB as radius, an arc is drawn to intersect the tangent,
t, at point C. AC is a close approximation to the length of the given arc
m.
10. To Divide a Circle into Seven Equal Parts by Concentric Circles. First,
draw a semicircle on OA as diameter. Then divide OA into seven equal parts
and construct verticals to intersect the semicircle in points 1, 2, etc.
Finally, draw the required concentric circles with radii 0-1, 0-2, 0-3,
etc.

D. Conic Sections
The Ellipse. The ellipse may be defined as the locus of all coplanar
points, the sum of whose distances from two fixed points (foci) is a constant.
1. To construct an ellipse when the foci F1 and F2 and the constant distant
AB are given. With F1 as center and radius AC (any portion of AB), an arc
is drawn. Now with F2 as center and radius CB, an arc is drawn intersecting
the first arc in points 1 and 2, which are two points on the ellipse.
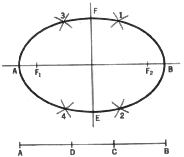
This construction is repeated for the location of additional points. For
example, with F1 as center and radius AD, an arc is drawn, and with F2 as
center and radius DB an intersecting arc is drawn, thus locating two additional
points 3 and 4. The smooth curve passing through these points and others
(not shown) is the ellipse. The major and minor axes are AB and EF, respectively.
2. To draw an ellipse by the pin-and-string method when the major axis,
AB, and the minor axis, CD, are given. With center C and radius equal to
OA draw an arc intersecting the major axis at points F1 and F2, which are
the foci. Now fix the ends of a string at points F1 and F2, such that the
length of the string is equal to AB. For any point on the ellipse, such
as point P or P, the sum of distances PF1 and PF2 (or of P'F1 and P'F2)
remains equal to the constant length of the string. Therefore, the ellipse
is easily drawn by maintaining taut segments of the string, as a pencil
(or other marking device) is used to draw the curve.
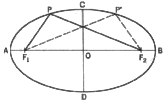
3. To draw an ellipse when two conjugate axes are given. Let us assume lines
AB and CD as the given conjugate axes (each axis is parallel to the tangents
to the ellipse at the end points of the other axis). Lines drawn through
points C and D, parallel to axis AB, are tangent to the ellipse at these
points; and, similarly, lines drawn through points A and B, parallel to
axis CD, are tangent to the ellipse at points A and B. The parallelogram
formed by the four tangents circumscribes the required ellipse. Once the
major and minor axes are located we can establish the positions of the foci,
and then describe the ellipse. The following construction is used to locate
the major and minor axes of the ellipse. Through D draw DE perpendicular
to AB and equal to OB. Draw OE and describe a circle with radius M2O (or
M2E). Now draw line DM2 to intersect the circle at points G and K. The minor
axis, NN1, of the ellipse contains line KO, and the major axis, MM1, contains
line GO. Length ON (or ON1), the semiminor axis, is equal to length DG,
and OM (or OM1), the semimajor axis, is equal to length DK. The foci are
easily located. With N as center and radius OM, describe an arc to intersect
the major axis at the foci F and F1. The ellipse may now be constructed.
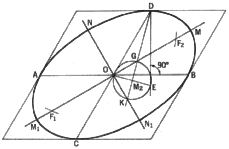
4. To determine the major and minor axes, and the foci of a given ellipse.
First draw two parallels such as m and n. Now draw AB, which bisects lines
m and n. Locate O, the midpoint of AB. With O as center and radius OA, draw
a circle to intersect the ellipse at points C and B. Through O draw a line
NN1 parallel to line CA and draw line MM1 perpendicular to CA. Lines NN1
and MM1 are the minor and major axes, respectively.
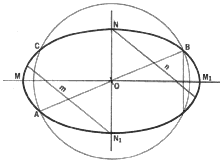
5. To draw an ellipse by the concentric circle method, given the lengths
of the major and minor axes. Lines AB and CD are the major and minor axes,
respectively. Through point O, the center of the ellipse, draw radial lines
such as m to intersect the concentric circles having radii OB and OC in
points E, F, G, and K. Through points E and F draw vertical lines to intersect
the horizontals drawn through G and K, in points P and Q, which are two
points on the ellipse. Repeat this construction for additional points and
then draw a smooth curve through these points to form the ellipse.
The tangent, t, at point P passes through point R, which is the intersection
of the tangent t' at point E of the major circle and the major axis extended.
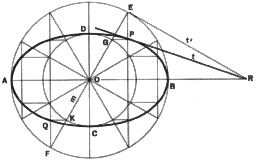
6. To draw an ellipse by the trammel method when the major and minor axes
are given. First a strip is marked with distance O'B'' equal to OB and O'C''
equal to OC. Now the strip is moved so that point B' travels along the minor
axis while C' moves along the major axis. For any such position, O' will
locate a point on the ellipse.
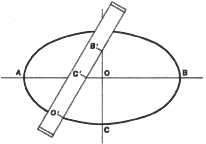
7. To draw an ellipse by the use of circular arcs when the axes are given.
This will result in a close approximation to a true ellipse. Join points
A and C. Lay off distance CD equal to CE (where CE = 0A-OC). Now draw the
perpendicular bisector of AD and locate points G and K. With G as center
and radius GA, describe arc TAT1. With K as center and radius KT, describe
arc TCT2. Center G' and radius G'B are used to draw arc T2BT3; and center
K' and radius K'T3 are used to draw arc T3T1.
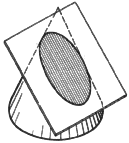
8. To inscribe an ellipse in a given rectangle. Divide OA into a number
of equal parts (four are shown), and then divide AE into the same number
of equal parts. Now draw rays D-1, D-2, etc., to intersect the corresponding
rays C-1, C-2, etc., in points which lie on the ellipse. The construction
shown may be repeated for the other quarters of the rectangle in order to
obtain additional points on the ellipse. The pictorial shows a right circular
cone intersected by an inclined plane that cuts all the elements of the
cone. The intersection is an ellipse.
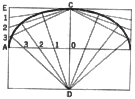
The Parabola. A parabola is a plane curve any point of which is the
same distance from a point called the focus as it is from a straight line
known as the directrix.
1. To locate points on a parabola when the focus, F, and the directrix,
d, are given. Points such as 1 and 2 are determined by locating the intersection
of line s (any line parallel to the directrix) and an arc having center
F and a radius equal to the distance between the parallel lines d and s.
Now it is quite apparent that points 1 and 2 are the same distance from
F, the focus, as they are from d, the directrix. The tangent, t, at point
P bisects the angle KPF.
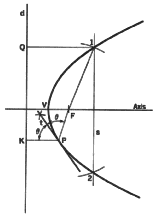
2. To determine the axis, focus, and directrix of a given parabola. The
axis is located in the following manner. Draw two parallel chords such as
m and n. The line t joining the midpoints of these chords is parallel to
the axis. Now introduce a line such as s perpendicular to line t. The required
axis is the perpendicular bisector of line s. The focus, F, is located by
making angle FTC equal to angle CTA. Point C is the intersection of the
axis with the perpendicular to tangent line k at point T. The directrix,
d, is perpendicular to the axis and at a distance from V equal to VF, that
is, VB = VF.
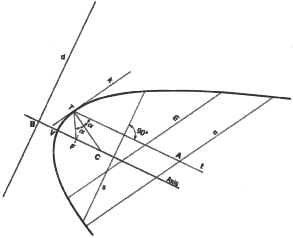
3. To construct a parabola, given the axis, vertex V, and a point P through
which the parabola passes. First draw rectangle PABC. Now divide
CP and CV into the same number of equal parts. Introduce lines parallel
to the axis and passing through points 1, 2, and 3 on side VC. Draw rays
V-1, V-2, and V-3. Finally locate the points in which the parallels intersect
the corresponding rays, i.e., the parallel through point 1 intersects ray
V-1, etc. The curve through the points thus located is the parabola. The
pictorial shows a right circular cone intersected by a plane parallel to
an element of the cone. The intersection is a parabola.
The Hyperbola. The hyperbola may be defined as the locus of all coplanar
points the differences of whose distances from two fixed points (foci) is
a constant.
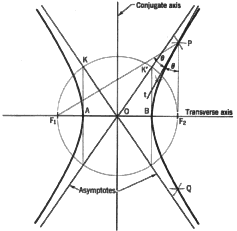
1. To construct a hyperbola when the foci, F1 and F2, and the constant distance,
AB, are given. With F1 as center and a radius greater than FIB, an arc is
drawn. Now with F2 as center and a radius which is equal to the difference
between the first radius and length AB, an arc is drawn to intersect the
first arc in points P and Q, which are two points on the hyperbola. It is
clearly seen that F1P-F2P = AB and that F1Q-F2Q = AB. Additional points
may be found in a similar manner. The smooth curve passing through the points
is the hyperbola. It should be noted that the curve has two branches which
are symmetrical with respect to the axes. The asymptotes pass through the
center O and are tangent to the curve at infinity. They are located by joining
point O the center of the hyperbola with points K and K'. These points are
found by locating the intersections of the verticals through points A and
B with the circle of radius OFT. The tangent, t, at point P bisects the
angle F2PF1.
2. To construct a rectangular hyperbola (asymptotes are at right angles),
given the asymptotes m and n, and one point P on the curve. Draw lines k
and t through point P, respectively parallel to n and m. Select any point
Q on line k and then draw line OQ. Locate point R, the intersection of OQ
and t. Draw a horizontal line through point R and a vertical line through
point Q. The intersection of these lines is point S, a point on the hyperbola.
In a similar manner additional points are located.
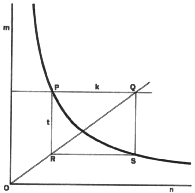
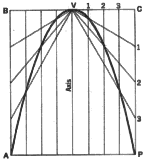
3. To construct a hyperbola, given the transverse axis AB, and a point P
on the curve. First construct the rectangle PCDE. Now divide
side EP into a number of equal parts (four are shown) and the right half
of side CP into the same number of equal parts. Find the intersection of
rays A-1, A-2, etc., with the corresponding rays B-1, B-2, etc. Repeat the
procedure for the left half of the rectangle. The smooth curve which passes
through the points thus located is one branch of the hyperbola. The other
branch may be determined in a similar manner. The pictorial shows a right
circular cone intersected by a plane parallel to the axis of the cone. The
intersection is a hyperbola (one branch shown).

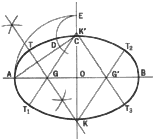
Pascal and His Theorem. In 1640, at the age of 16, Pascal discovered
the relationship that "the opposite sides of a hexagon, which is inscribed
in a conic, intersect in points that lie on one line." For example,
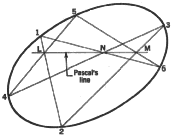
the sides of the inscribed hexagon are 1-2, 2-3, 3-4, 4-5, 5-6, and 6-1.
Opposite sides 1-2 and 4-5 intersect at point L; opposite sides 2-3 and
5-6 intersect at point M; and opposite sides 3-4 and 6-1 intersect at point
N. The line which passes through points L, M, and N is known as Pascal's
line.
1. To locate a sixth point on a conic when five points are known. Let us
suppose that points 1, 2, 3, 4, and 5 are known and that it is required
to locate a sixth point, K. Basing our construction upon Pascal's theorem,
we can first establish point L which is the intersection of the opposite
sides 1-2 and 4-5 of the inscribed hexagon 1, 2, 3, 4, 5, K. Now we know
that another pair of opposite sides is 2-3 and 5-K. Therefore, we may draw
any line through point 5 to intersect side 2-3 in point M. We know that
point K is somewhere on line 5-M. We also know that Pascal's line passes
through points L and M. The third pair of opposite sides is 3-4 and K-1.
If we join points 3 and 4, then line 3-4 must intersect Pascal's line in
a point, N, through which side K-1 must pass. It is now seen that lines
1-N and 5-M must intersect at point K, which is a sixth point on the conic.
Additional points may be located by drawing other lines through point 5
to intersect side 2-3 in a new M-point, and then repeating the construction
described above.
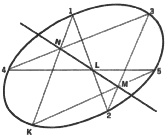
2. To locate points on a conic that passes through a given point and is
tangent to given lines at two points. It is assumed that the conic passes
through the given point 3 and tangent to lines t and t'' at points 2 and
4, respectively. We recall that when five points on a conic
are known it is possible to locate a sixth point. How can we reduce the
problem shown to the previous one? How shall we establish five
known points on the conic, when apparently only three are given?
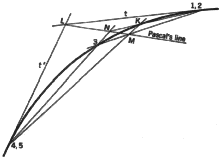
If point 5, for example,

were moved along the curve until it coincided with point 4, chord 4-5 would
become a tangent to the curve at point 4. Therefore, we can show point 5,
coincident with point 4. Similarly, points 2 and 1 are coincident.
Now the intersection of opposite sides 1-2(t) and 4-5(t'') of the inscribed
hexagon 1, 2, 3, 4, 5, K (K is a sixth point on the conic) is point L. The
intersection of opposite sides, 2-3 and 5-K, is point M. If we take M as
any point on side 2-3, we know that point K is somewhere on line 5-M. The
line joining points L and M is a Pascal line. We know that the opposite
sides, 3-4 and K-1, must meet on the Pascal line; therefore, the intersection
of side 3-4 with the Pascal line is point N, through which side 1-K must
pass. Therefore, the intersection of lines 1-N and 5-M is point K, another
point on the conic. Additional points may be located in a similar manner.
3. To construct a tangent to a given conic at a point of the conic. Let
us construct the tangent to the conic at point P. Inscribe a hexagon 1,
2, 3, 4, 5, 6 such that side 5-6 will be the tangent. Two points L and M
of the Pascal line are located by finding the intersection of sides 1-2
and 4-5, and of sides 3-4 and 6-1, respectively. Sides 23 and 5-6 must meet
on the Pascal line, at point N, which is located by finding the intersection
of side 2-3 with the Pascal line. The required tangent is line NP.

Brianchon's Theorem. This theorem, which is most useful in locating
tangents to a conic, states that "the three lines joining the three
pairs of opposite vertices of a hexagon circumscribed about a conic meet
in a point."
Line AB joins the pair of opposite vertices determined by tangents 1 and
2, and 4 and 5. Similarly line CD joins the pair of opposite vertices determined
by tangents 2 and 3, and 5 and 6. Lines AB and CD intersect in Brianchon's
point, P. Line EF, which joins the remaining pair of opposite vertices,
also passes through point P.
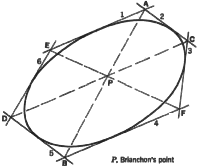
1. To determine a sixth tangent to a conic when five tangents (sides of
the circumscribed hexagon) are given. Suppose that tangents 1, 2, 3, 4,
and 5 are given. It is required to locate a sixth side of a circumscribed
hexagon. Line AB, which joins one pair of opposite vertices, is easily determined.
Now through point C (the intersection of tangents 2 and 3) a line is drawn
intersecting AB at point P (Brianchon's point). Line CP intersects tangent
5 at point D. Line FP intersects tangent 1 at point E. Line DE is the required
tangent or sixth side of the circumscribed hexagon.
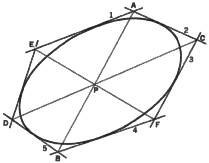
2. To determine the point of contact of a tangent to a conic. Suppose we
wish to locate the point of tangency of tangent 1. If tangent 2 approaches
tangent 1 as a limiting position, the point of intersection of tangents
1 and 2 approaches the contact point of tangent 1 with the conic. Let us
denote this point as point 6. Now we may make use of Brianchon's point to
locate point 6. The intersection of lines I and m determines Brianchon's
point, P. Line n passes through point P and the intersection of tangents
3 and 4. Point 6, the required point of contact of tangent 1 with the conic,
is at the intersection of line n with the tangent line
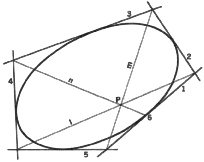
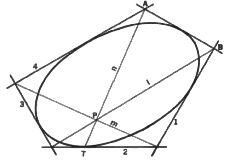
3. To determine additional tangents to a conic when four tangents and the
point of contact on one of them are known. The four given tangents are 1,
2, 3, and 4, and the point of contact on tangent 2 is point T. Line m is
determined by joining the pair of opposite vertices that is given. Tangent
2 is actually two tangents that intersect at point T. Now through point
T a line n is drawn to intersect line m at point P (a Brianchon's point),
and tangent 4 at point A. Line I is drawn through the common point of tangents
2 and 3 and point P to intersect tangent 1 at point B. Line AB is an additional
tangent to the conic. In a similar manner more tangents may be determined.
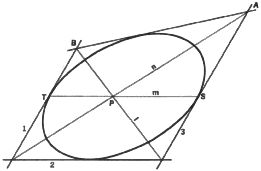
4. To determine additional tangents to a conic when three tangents and the
points of contact on two of them are known. The three known tangents are
1, 2, and 3, and the points of contact, points S and T. Line m joins points
S and T. Now through the intersection of tangents 1 and 2 draw a line n
to intersect line m at point P (a Brianchon's point) and to intersect tangent
3 at point A. Finally draw line I through the common point of tangents 2
and 3, and point P to intersect tangent 1 at point B. Line ABis an additional
tangent to the conic.
Additional Useful Geometric Constructions.
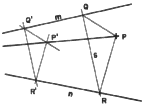
1. To draw a line through a given point, P, and the inaccessible copoint
of given lines m and n. Draw a line such as s to intersect m and n at points
Q and R, respectively. Form triangle PQR. Now select a point such as Q'
on line m and draw through Q' lines respectively parallel to QP and QR.
Through R' draw a line parallel to RP and form the triangle P'Q'R''. The
line, PP', is the solution.
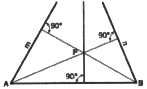
2. To draw a line perpendicular to a given line AB and through the inaccessible
copoint of given lines m and n that pass through points A and B, respectively.
Through points B and A draw lines respectively perpendicular to m and n,
and intersecting at point P. Now construct the required line through point
P perpendicular to line AB.
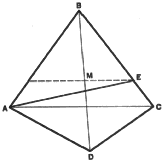
3. To divide a given quadrilateral ABCD into two equal areas by a line which
passes through one of the corners, A. Draw line BD and locate its midpoint,
M. Draw a line through point M parallel to diagonal AC to intersect side
BC at point E. Line AE divides the quadrilateral into equal areas AEB and
AECD.












 .
. 







































